|
ADMB Documentation
11.5.3197
|
|
ADMB Documentation
11.5.3197
|
Functions | |
| dvariable | generalized_Ricker1 (const double &x, const prevariable &x0, const prevariable &A, const prevariable &alpha) |
| generalized Ricker function, first parameerization; scalar | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const prevariable &x0, const prevariable &A, const prevariable &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const dvar_vector &x0, const prevariable &A, const prevariable &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const prevariable &x0, const dvar_vector &A, const prevariable &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const dvar_vector &x0, const dvar_vector &A, const prevariable &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const prevariable &x0, const prevariable &A, const dvar_vector &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const dvar_vector &x0, const prevariable &A, const dvar_vector &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const prevariable &x0, const dvar_vector &A, const dvar_vector &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| dvar_vector | generalized_Ricker1 (const dvector &x, const dvar_vector &x0, const dvar_vector &A, const dvar_vector &alpha) |
| generalized Ricker function, first parameerization; vectorized | |
| df1b2variable | generalized_Ricker1 (const double &x, const df1b2variable &x0, const df1b2variable &A, const df1b2variable &alpha) |
| generalized Ricker function, first parameerization; random effects scalar | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2variable &x0, const df1b2variable &A, const df1b2variable &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2vector &x0, const df1b2variable &A, const df1b2variable &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2variable &x0, const df1b2vector &A, const df1b2variable &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2vector &x0, const df1b2vector &A, const df1b2variable &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2variable &x0, const df1b2variable &A, const df1b2vector &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2vector &x0, const df1b2variable &A, const df1b2vector &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2variable &x0, const df1b2vector &A, const df1b2vector &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker1 (const dvector &x, const df1b2vector &x0, const df1b2vector &A, const df1b2vector &alpha) |
| generalized Ricker function, first parameerization; random effects vectorized | |
| dvariable | generalized_Ricker2 (const double &x, const prevariable &r, const prevariable &a, const prevariable &alpha) |
| generalized Ricker function, second parameerization; scalar | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const prevariable &r, const prevariable &a, const prevariable &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const dvar_vector &r, const prevariable &a, const prevariable &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const prevariable &r, const dvar_vector &a, const prevariable &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const dvar_vector &r, const dvar_vector &a, const prevariable &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const prevariable &r, const prevariable &a, const dvar_vector &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const dvar_vector &r, const prevariable &a, const dvar_vector &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const prevariable &r, const dvar_vector &a, const dvar_vector &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| dvar_vector | generalized_Ricker2 (const dvector &x, const dvar_vector &r, const dvar_vector &a, const dvar_vector &alpha) |
| generalized Ricker function, second parameerization; vectorized | |
| df1b2variable | generalized_Ricker2 (const double &x, const df1b2variable &r, const df1b2variable &a, const df1b2variable &alpha) |
| generalized Ricker function, second parameerization; random effects scalar | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2variable &r, const df1b2variable &a, const df1b2variable &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2vector &r, const df1b2variable &a, const df1b2variable &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2variable &r, const df1b2vector &a, const df1b2variable &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2vector &r, const df1b2vector &a, const df1b2variable &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2variable &r, const df1b2variable &a, const df1b2vector &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2vector &r, const df1b2variable &a, const df1b2vector &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2variable &r, const df1b2vector &a, const df1b2vector &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| df1b2vector | generalized_Ricker2 (const dvector &x, const df1b2vector &r, const df1b2vector &a, const df1b2vector &alpha) |
| generalized Ricker function, second parameerization; random effects vectorized | |
| dvariable | Gompertz (const double &x, const prevariable &a, const prevariable &b) |
| Gompertz function; scalar. | |
| dvar_vector | Gompertz (const dvector &x, const prevariable &a, const prevariable &b) |
| Gompertz function; vectorized. | |
| dvar_vector | Gompertz (const dvector &x, const dvar_vector &a, const prevariable &b) |
| Gompertz function; vectorized. | |
| dvar_vector | Gompertz (const dvector &x, const prevariable &a, const dvar_vector &b) |
| Gompertz function; vectorized. | |
| dvar_vector | Gompertz (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| Gompertz function; vectorized. | |
| df1b2variable | Gompertz (const double &x, const df1b2variable &a, const df1b2variable &b) |
| Gompertz function; random effects scalar. | |
| df1b2vector | Gompertz (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| Gompertz function; random effects vectorized. | |
| df1b2vector | Gompertz (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| Gompertz function; random effects vectorized. | |
| df1b2vector | Gompertz (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| Gompertz function; random effects vectorized. | |
| df1b2vector | Gompertz (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| Gompertz function; random effects vectorized. | |
| dvariable | Hassell (const double &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Hassell function scalar. | |
| dvar_vector | Hassell (const dvector &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const dvar_vector &a, const prevariable &b, const prevariable &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const prevariable &a, const dvar_vector &b, const prevariable &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const dvar_vector &a, const dvar_vector &b, const prevariable &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const prevariable &a, const prevariable &b, const dvar_vector &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const dvar_vector &a, const prevariable &b, const dvar_vector &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const prevariable &a, const dvar_vector &b, const dvar_vector &c) |
| Hassell function vectorized. | |
| dvar_vector | Hassell (const dvector &x, const dvar_vector &a, const dvar_vector &b, const dvar_vector &c) |
| Hassell function vectorized. | |
| df1b2variable | Hassell (const double &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Hassell function random effects scalar. | |
| df1b2vector | Hassell (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2variable &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2variable &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2variable &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2vector &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2vector &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2vector &c) |
| Hassell function random effects vectorized. | |
| df1b2vector | Hassell (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2vector &c) |
| Hassell function random effects vectorized. | |
| dvariable | Hill (const double &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Hill function; scalar. | |
| dvar_vector | Hill (const dvector &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const dvar_vector &a, const prevariable &b, const prevariable &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const prevariable &a, const dvar_vector &b, const prevariable &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const dvar_vector &a, const dvar_vector &b, const prevariable &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const prevariable &a, const prevariable &b, const dvar_vector &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const dvar_vector &a, const prevariable &b, const dvar_vector &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const prevariable &a, const dvar_vector &b, const dvar_vector &c) |
| Hill function; vectorized. | |
| dvar_vector | Hill (const dvector &x, const dvar_vector &a, const dvar_vector &b, const dvar_vector &c) |
| Hill function; vectorized. | |
| df1b2variable | Hill (const double &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Hill function; random effects scalar. | |
| df1b2vector | Hill (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2variable &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2variable &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2variable &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2vector &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2vector &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2vector &c) |
| Hill function; random effects vectorized. | |
| df1b2vector | Hill (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2vector &c) |
| Hill function; random effects vectorized. | |
| dvariable | HollingII (const double &x, const prevariable &alpha, const prevariable &h) |
| HollingII scalar. | |
| dvar_vector | HollingII (const dvector &x, const prevariable &alpha, const prevariable &h) |
| HollingII vectorized. | |
| dvar_vector | HollingII (const dvector &x, const dvar_vector &alpha, const prevariable &h) |
| HollingII vectorized. | |
| dvar_vector | HollingII (const dvector &x, const prevariable &alpha, const dvar_vector &h) |
| HollingII vectorized. | |
| dvar_vector | HollingII (const dvector &x, const dvar_vector &alpha, const dvar_vector &h) |
| HollingII vectorized. | |
| df1b2variable | HollingII (const double &x, const df1b2variable &alpha, const df1b2variable &h) |
| HollingII random effects scalar. | |
| df1b2vector | HollingII (const dvector &x, const df1b2variable &alpha, const df1b2variable &h) |
| HollingII random effects vectorized. | |
| df1b2vector | HollingII (const dvector &x, const df1b2vector &alpha, const df1b2variable &h) |
| HollingII random effects vectorized. | |
| df1b2vector | HollingII (const dvector &x, const df1b2variable &alpha, const df1b2vector &h) |
| HollingII random effects vectorized. | |
| df1b2vector | HollingII (const dvector &x, const df1b2vector &alpha, const df1b2vector &h) |
| HollingII random effects vectorized. | |
| dvariable | HollingIII (const double &x, const prevariable &a, const prevariable &b) |
| Holling Type III function; scalar. | |
| dvar_vector | HollingIII (const dvector &x, const prevariable &a, const prevariable &b) |
| Holling Type III function; vectorized. | |
| dvar_vector | HollingIII (const dvector &x, const dvar_vector &a, const prevariable &b) |
| Holling Type III function; vectorized. | |
| dvar_vector | HollingIII (const dvector &x, const prevariable &a, const dvar_vector &b) |
| Holling Type III function; vectorized. | |
| dvar_vector | HollingIII (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| Holling Type III function; vectorized. | |
| df1b2variable | HollingIII (const double &x, const df1b2variable &a, const df1b2variable &b) |
| Holling Type III function; random effects scalar. | |
| df1b2vector | HollingIII (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| Holling Type III function; random effects vectorized. | |
| df1b2vector | HollingIII (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| Holling Type III function; random effects vectorized. | |
| df1b2vector | HollingIII (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| Holling Type III function; random effects vectorized. | |
| df1b2vector | HollingIII (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| Holling Type III function; random effects vectorized. | |
| dvariable | HollingIV (const double &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Holling Type IV function; scalar. | |
| dvar_vector | HollingIV (const dvector &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const dvar_vector &a, const prevariable &b, const prevariable &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const prevariable &a, const dvar_vector &b, const prevariable &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const dvar_vector &a, const dvar_vector &b, const prevariable &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const prevariable &a, const prevariable &b, const dvar_vector &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const dvar_vector &a, const prevariable &b, const dvar_vector &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const prevariable &a, const dvar_vector &b, const dvar_vector &c) |
| Holling Type IV function; vectorized. | |
| dvar_vector | HollingIV (const dvector &x, const dvar_vector &a, const dvar_vector &b, const dvar_vector &c) |
| Holling Type IV function; vectorized. | |
| df1b2variable | HollingIV (const double &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Holling Type IV function; random effects scalar. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2variable &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2variable &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2variable &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2vector &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2vector &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2vector &c) |
| Holling Type IV function; random effects vectorized. | |
| df1b2vector | HollingIV (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2vector &c) |
| Holling Type IV function; random effects vectorized. | |
| dvariable | logistic (const double &x, const prevariable &a, const prevariable &b) |
| logistic function; scalar | |
| dvar_vector | logistic (const dvector &x, const prevariable &a, const prevariable &b) |
| logistic function; vectorized | |
| dvar_vector | logistic (const dvector &x, const dvar_vector &a, const prevariable &b) |
| logistic function; vectorized | |
| dvar_vector | logistic (const dvector &x, const prevariable &a, const dvar_vector &b) |
| logistic function; vectorized | |
| dvar_vector | logistic (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| logistic function; vectorized | |
| df1b2variable | logistic (const double &x, const df1b2variable &a, const df1b2variable &b) |
| logistic function; random effects scalar | |
| df1b2vector | logistic (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| logistic function; random effects vectorized | |
| df1b2vector | logistic (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| logistic function; random effects vectorized | |
| df1b2vector | logistic (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| logistic function; random effects vectorized | |
| df1b2vector | logistic (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| logistic function; random effects vectorized | |
| dvariable | logistic3 (const double &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| logistic function with carrying capacity c; scalar | |
| dvar_vector | logistic3 (const dvector &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const dvar_vector &a, const prevariable &b, const prevariable &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const prevariable &a, const dvar_vector &b, const prevariable &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const dvar_vector &a, const dvar_vector &b, const prevariable &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const prevariable &a, const prevariable &b, const dvar_vector &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const dvar_vector &a, const prevariable &b, const dvar_vector &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const prevariable &a, const dvar_vector &b, const dvar_vector &c) |
| logistic function with carrying capacity c; vectorized | |
| dvar_vector | logistic3 (const dvector &x, const dvar_vector &a, const dvar_vector &b, const dvar_vector &c) |
| logistic function with carrying capacity c; vectorized | |
| df1b2variable | logistic3 (const double &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| logistic function with carrying capacity c; random effects scalar | |
| df1b2vector | logistic3 (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2variable &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2variable &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2variable &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2vector &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2vector &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2vector &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| df1b2vector | logistic3 (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2vector &c) |
| logistic function with carrying capacity c; random effects vectorized | |
| dvariable | logisticK (const double &t, const prevariable &K, const prevariable &r, const prevariable &n0) |
| ecologically parameterized logistic function with carrying capacity K; scalar | |
| dvar_vector | logisticK (const dvector &t, const prevariable &K, const prevariable &r, const prevariable &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const dvar_vector &K, const prevariable &r, const prevariable &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const prevariable &K, const dvar_vector &r, const prevariable &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const dvar_vector &K, const dvar_vector &r, const prevariable &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const prevariable &K, const prevariable &r, const dvar_vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const dvar_vector &K, const prevariable &r, const dvar_vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const prevariable &K, const dvar_vector &r, const dvar_vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| dvar_vector | logisticK (const dvector &t, const dvar_vector &K, const dvar_vector &r, const dvar_vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; vectorized | |
| df1b2variable | logisticK (const double &t, const df1b2variable &K, const df1b2variable &r, const df1b2variable &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects scalar | |
| df1b2vector | logisticK (const dvector &t, const df1b2variable &K, const df1b2variable &r, const df1b2variable &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2vector &K, const df1b2variable &r, const df1b2variable &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2variable &K, const df1b2vector &r, const df1b2variable &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2vector &K, const df1b2vector &r, const df1b2variable &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2variable &K, const df1b2variable &r, const df1b2vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2vector &K, const df1b2variable &r, const df1b2vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2variable &K, const df1b2vector &r, const df1b2vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| df1b2vector | logisticK (const dvector &t, const df1b2vector &K, const df1b2vector &r, const df1b2vector &n0) |
| ecologically parameterized logistic function with carrying capacity K; random effects vectorized | |
| dvariable | Michaelis_Menten1 (const double &x, const prevariable &a, const prevariable &b) |
| Michaelis Menten function, 1st parametarization; scalar. | |
| dvar_vector | Michaelis_Menten1 (const dvector &x, const prevariable &a, const prevariable &b) |
| Michaelis Menten function, 1st parametarization; vectorized. | |
| dvar_vector | Michaelis_Menten1 (const dvector &x, const dvar_vector &a, const prevariable &b) |
| Michaelis Menten function, 1st parametarization; vectorized. | |
| dvar_vector | Michaelis_Menten1 (const dvector &x, const prevariable &a, const dvar_vector &b) |
| Michaelis Menten function, 1st parametarization; vectorized. | |
| dvar_vector | Michaelis_Menten1 (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| Michaelis Menten function, 1st parametarization; vectorized. | |
| df1b2variable | Michaelis_Menten1 (const double &x, const df1b2variable &a, const df1b2variable &b) |
| Michaelis Menten function, 1st parametarization; random effects scalar. | |
| df1b2vector | Michaelis_Menten1 (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| Michaelis Menten function, 1st parametarization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten1 (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| Michaelis Menten function, 1st parametarization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten1 (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| Michaelis Menten function, 1st parametarization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten1 (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| Michaelis Menten function, 1st parametarization; random effects vectorized. | |
| dvariable | Michaelis_Menten2 (const double &x, const prevariable &a, const prevariable &b) |
| Michaelis Menten function, 2nd parameterization; scalar. | |
| dvar_vector | Michaelis_Menten2 (const dvector &x, const prevariable &a, const prevariable &b) |
| Michaelis Menten function, 2nd parameterization; vectorized. | |
| dvar_vector | Michaelis_Menten2 (const dvector &x, const dvar_vector &a, const prevariable &b) |
| Michaelis Menten function, 2nd parameterization; vectorized. | |
| dvar_vector | Michaelis_Menten2 (const dvector &x, const prevariable &a, const dvar_vector &b) |
| Michaelis Menten function, 2nd parameterization; vectorized. | |
| dvar_vector | Michaelis_Menten2 (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| Michaelis Menten function, 2nd parameterization; vectorized. | |
| df1b2variable | Michaelis_Menten2 (const double &x, const df1b2variable &a, const df1b2variable &b) |
| Michaelis Menten function, 2nd parameterization; random effects scalar. | |
| df1b2vector | Michaelis_Menten2 (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| Michaelis Menten function, 2nd parameterization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten2 (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| Michaelis Menten function, 2nd parameterization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten2 (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| Michaelis Menten function, 2nd parameterization; random effects vectorized. | |
| df1b2vector | Michaelis_Menten2 (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| Michaelis Menten function, 2nd parameterization; random effects vectorized. | |
| dvariable | monomolecular (const double &x, const prevariable &a, const prevariable &b) |
| monomoleular function; scalar | |
| dvar_vector | monomolecular (const dvector &x, const prevariable &a, const prevariable &b) |
| monomoleular function; vectorized | |
| dvar_vector | monomolecular (const dvector &x, const dvar_vector &a, const prevariable &b) |
| monomoleular function; vectorized | |
| dvar_vector | monomolecular (const dvector &x, const prevariable &a, const dvar_vector &b) |
| monomoleular function; vectorized | |
| dvar_vector | monomolecular (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| monomoleular function; vectorized | |
| df1b2variable | monomolecular (const double &x, const df1b2variable &a, const df1b2variable &b) |
| monomoleular function; random effects scalar | |
| df1b2vector | monomolecular (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| monomoleular function; random effects vectorized | |
| df1b2vector | monomolecular (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| monomoleular function; random effects vectorized | |
| df1b2vector | monomolecular (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| monomoleular function; random effects vectorized | |
| df1b2vector | monomolecular (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| monomoleular function; random effects vectorized | |
| dvariable | nonrectangular_hyperbola (const double &x, const prevariable &theta, const prevariable &alpha, const prevariable &pmax) |
| nonrectangular hyperbolic function; scalar | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const prevariable &theta, const prevariable &alpha, const prevariable &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const dvar_vector &theta, const prevariable &alpha, const prevariable &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const prevariable &theta, const dvar_vector &alpha, const prevariable &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const dvar_vector &theta, const dvar_vector &alpha, const prevariable &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const prevariable &theta, const prevariable &alpha, const dvar_vector &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const dvar_vector &theta, const prevariable &alpha, const dvar_vector &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const prevariable &theta, const dvar_vector &alpha, const dvar_vector &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| dvar_vector | nonrectangular_hyperbola (const dvector &x, const dvar_vector &theta, const dvar_vector &alpha, const dvar_vector &pmax) |
| nonrectangular hyperbolic function; vectorized | |
| df1b2variable | nonrectangular_hyperbola (const double &x, const df1b2variable &theta, const df1b2variable &alpha, const df1b2variable &pmax) |
| nonrectangular hyperbolic function; random effects scalar | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2variable &theta, const df1b2variable &alpha, const df1b2variable &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2vector &theta, const df1b2variable &alpha, const df1b2variable &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2variable &theta, const df1b2vector &alpha, const df1b2variable &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2vector &theta, const df1b2vector &alpha, const df1b2variable &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2variable &theta, const df1b2variable &alpha, const df1b2vector &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2vector &theta, const df1b2variable &alpha, const df1b2vector &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2variable &theta, const df1b2vector &alpha, const df1b2vector &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| df1b2vector | nonrectangular_hyperbola (const dvector &x, const df1b2vector &theta, const df1b2vector &alpha, const df1b2vector &pmax) |
| nonrectangular hyperbolic function; random effects vectorized | |
| dvariable | Ricker (const double &x, const prevariable &a, const prevariable &b) |
| Ricker function; scalar. | |
| dvar_vector | Ricker (const dvector &x, const prevariable &a, const prevariable &b) |
| Ricker function; vectorized. | |
| dvar_vector | Ricker (const dvector &x, const dvar_vector &a, const prevariable &b) |
| Ricker function; vectorized. | |
| dvar_vector | Ricker (const dvector &x, const prevariable &a, const dvar_vector &b) |
| Ricker function; vectorized. | |
| dvar_vector | Ricker (const dvector &x, const dvar_vector &a, const dvar_vector &b) |
| Ricker function; vectorized. | |
| df1b2variable | Ricker (const double &x, const df1b2variable &a, const df1b2variable &b) |
| Ricker function; random effects scalar. | |
| df1b2vector | Ricker (const dvector &x, const df1b2variable &a, const df1b2variable &b) |
| Ricker function; random effects vectorized. | |
| df1b2vector | Ricker (const dvector &x, const df1b2vector &a, const df1b2variable &b) |
| Ricker function; random effects vectorized. | |
| df1b2vector | Ricker (const dvector &x, const df1b2variable &a, const df1b2vector &b) |
| Ricker function; random effects vectorized. | |
| df1b2vector | Ricker (const dvector &x, const df1b2vector &a, const df1b2vector &b) |
| Ricker function; random effects vectorized. | |
| dvariable | Shepherd (const double &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Shepherd function scalar. | |
| dvar_vector | Shepherd (const dvector &x, const prevariable &a, const prevariable &b, const prevariable &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const dvar_vector &a, const prevariable &b, const prevariable &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const prevariable &a, const dvar_vector &b, const prevariable &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const dvar_vector &a, const dvar_vector &b, const prevariable &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const prevariable &a, const prevariable &b, const dvar_vector &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const dvar_vector &a, const prevariable &b, const dvar_vector &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const prevariable &a, const dvar_vector &b, const dvar_vector &c) |
| Shepherd function vectorized. | |
| dvar_vector | Shepherd (const dvector &x, const dvar_vector &a, const dvar_vector &b, const dvar_vector &c) |
| Shepherd function vectorized. | |
| df1b2variable | Shepherd (const double &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Shepherd function random effects scalar. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2variable &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2variable &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2variable &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2variable &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2variable &a, const df1b2variable &b, const df1b2vector &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2vector &a, const df1b2variable &b, const df1b2vector &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2variable &a, const df1b2vector &b, const df1b2vector &c) |
| Shepherd function random effects vectorized. | |
| df1b2vector | Shepherd (const dvector &x, const df1b2vector &a, const df1b2vector &b, const df1b2vector &c) |
| Shepherd function random effects vectorized. | |
| dvariable | theta_logistic (const double &t, const prevariable &K, const prevariable &r, const prevariable &n0, const prevariable &theta) |
| theta logistic function; scalar | |
| dvar_vector | theta_logistic (const dvector &t, const prevariable &K, const prevariable &r, const prevariable &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const dvar_vector &K, const prevariable &r, const prevariable &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const prevariable &K, const dvar_vector &r, const prevariable &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const dvar_vector &K, const dvar_vector &r, const prevariable &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const prevariable &K, const prevariable &r, const dvar_vector &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const dvar_vector &K, const prevariable &r, const dvar_vector &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const prevariable &K, const dvar_vector &r, const dvar_vector &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| dvar_vector | theta_logistic (const dvector &t, const dvar_vector &K, const dvar_vector &r, const dvar_vector &n0, const prevariable &theta) |
| theta logistic function; vectorized | |
| df1b2variable | theta_logistic (const double &t, const df1b2variable &K, const df1b2variable &r, const df1b2variable &n0, const df1b2variable &theta) |
| theta logistic function; random effects scalar | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2variable &K, const df1b2variable &r, const df1b2variable &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2vector &K, const df1b2variable &r, const df1b2variable &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2variable &K, const df1b2vector &r, const df1b2variable &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2vector &K, const df1b2vector &r, const df1b2variable &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2variable &K, const df1b2variable &r, const df1b2vector &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2vector &K, const df1b2variable &r, const df1b2vector &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2variable &K, const df1b2vector &r, const df1b2vector &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
| df1b2vector | theta_logistic (const dvector &t, const df1b2vector &K, const df1b2vector &r, const df1b2vector &n0, const df1b2variable &theta) |
| theta logistic function; random effects vectorized | |
Contributed by Mollie Brooks.
| dvariable generalized_Ricker1 | ( | const double & | x, |
| const prevariable & | x0, | ||
| const prevariable & | A, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; scalar
| x | independent variable; data scalar |
| x0 | ; differentiable scalar |
| A | ; differentiable scalar |
| alpha | ; differentiable scalar |

Definition at line 15 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const prevariable & | x0, | ||
| const prevariable & | A, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar |
| A | ; differentiable scalar |
| alpha | ; differentiable scalar |

Definition at line 32 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const dvar_vector & | x0, | ||
| const prevariable & | A, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector |
| A | ; differentiable scalar |
| alpha | ; differentiable scalar |

Definition at line 49 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const prevariable & | x0, | ||
| const dvar_vector & | A, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar |
| A | ; differentiable vector |
| alpha | ; differentiable scalar |

Definition at line 67 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const dvar_vector & | x0, | ||
| const dvar_vector & | A, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector |
| A | ; differentiable vector |
| alpha | ; differentiable scalar |

Definition at line 84 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const prevariable & | x0, | ||
| const prevariable & | A, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar |
| A | ; differentiable scalar |
| alpha | ; differentiable vector |

Definition at line 103 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const dvar_vector & | x0, | ||
| const prevariable & | A, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector |
| A | ; differentiable scalar |
| alpha | ; differentiable vector |

Definition at line 120 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const prevariable & | x0, | ||
| const dvar_vector & | A, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar |
| A | ; differentiable vector |
| alpha | ; differentiable vector |

Definition at line 138 of file generalized_Ricker1.cpp.
| dvar_vector generalized_Ricker1 | ( | const dvector & | x, |
| const dvar_vector & | x0, | ||
| const dvar_vector & | A, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector |
| A | ; differentiable vector |
| alpha | ; differentiable vector |

Definition at line 155 of file generalized_Ricker1.cpp.
| df1b2variable generalized_Ricker1 | ( | const double & | x, |
| const df1b2variable & | x0, | ||
| const df1b2variable & | A, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects scalar
| x | independent variable; data scalar |
| x0 | ; differentiable scalar in a random effects model |
| A | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |

Definition at line 175 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2variable & | x0, | ||
| const df1b2variable & | A, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar in a random effects model |
| A | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |

Definition at line 190 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2vector & | x0, | ||
| const df1b2variable & | A, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector in a random effects model |
| A | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |

Definition at line 205 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2variable & | x0, | ||
| const df1b2vector & | A, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar in a random effects model |
| A | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |

Definition at line 223 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2vector & | x0, | ||
| const df1b2vector & | A, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector in a random effects model |
| A | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |

Definition at line 238 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2variable & | x0, | ||
| const df1b2variable & | A, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar in a random effects model |
| A | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |

Definition at line 258 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2vector & | x0, | ||
| const df1b2variable & | A, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector in a random effects model |
| A | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |

Definition at line 273 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2variable & | x0, | ||
| const df1b2vector & | A, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable scalar in a random effects model |
| A | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |

Definition at line 291 of file generalized_Ricker1.cpp.
| df1b2vector generalized_Ricker1 | ( | const dvector & | x, |
| const df1b2vector & | x0, | ||
| const df1b2vector & | A, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, first parameerization; random effects vectorized
| x | independent variable; data vector |
| x0 | ; differentiable vector in a random effects model |
| A | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |

Definition at line 306 of file generalized_Ricker1.cpp.
| dvariable generalized_Ricker2 | ( | const double & | x, |
| const prevariable & | r, | ||
| const prevariable & | a, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; scalar
| x | independent variable; data scalar |
| r | ; differentiable scalar |
| a | ; differentiable scalar |
| alpha | ; differentiable scalar |
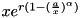
Definition at line 15 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const prevariable & | r, | ||
| const prevariable & | a, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar |
| a | ; differentiable scalar |
| alpha | ; differentiable scalar |
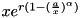
Definition at line 32 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const dvar_vector & | r, | ||
| const prevariable & | a, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable vector |
| a | ; differentiable scalar |
| alpha | ; differentiable scalar |
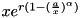
Definition at line 49 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const prevariable & | r, | ||
| const dvar_vector & | a, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar |
| a | ; differentiable vector |
| alpha | ; differentiable scalar |
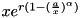
Definition at line 67 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const dvar_vector & | r, | ||
| const dvar_vector & | a, | ||
| const prevariable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable vector |
| a | ; differentiable vector |
| alpha | ; differentiable scalar |
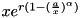
Definition at line 84 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const prevariable & | r, | ||
| const prevariable & | a, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar |
| a | ; differentiable scalar |
| alpha | ; differentiable vector |
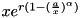
Definition at line 103 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const dvar_vector & | r, | ||
| const prevariable & | a, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable vector |
| a | ; differentiable scalar |
| alpha | ; differentiable vector |
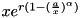
Definition at line 120 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const prevariable & | r, | ||
| const dvar_vector & | a, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar |
| a | ; differentiable vector |
| alpha | ; differentiable vector |
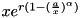
Definition at line 138 of file generalized_Ricker2.cpp.
| dvar_vector generalized_Ricker2 | ( | const dvector & | x, |
| const dvar_vector & | r, | ||
| const dvar_vector & | a, | ||
| const dvar_vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; vectorized
| x | independent variable; data vector |
| r | ; differentiable vector |
| a | ; differentiable vector |
| alpha | ; differentiable vector |
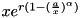
Definition at line 155 of file generalized_Ricker2.cpp.
| df1b2variable generalized_Ricker2 | ( | const double & | x, |
| const df1b2variable & | r, | ||
| const df1b2variable & | a, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects scalar
| x | independent variable; data scalar |
| r | ; differentiable scalar in a random effects model |
| a | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
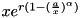
Definition at line 175 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2variable & | r, | ||
| const df1b2variable & | a, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar in a random effects model |
| a | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
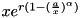
Definition at line 190 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2vector & | r, | ||
| const df1b2variable & | a, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable vector in a random effects model |
| a | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
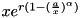
Definition at line 205 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2variable & | r, | ||
| const df1b2vector & | a, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar in a random effects model |
| a | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
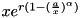
Definition at line 223 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2vector & | r, | ||
| const df1b2vector & | a, | ||
| const df1b2variable & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable vector in a random effects model |
| a | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
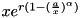
Definition at line 238 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2variable & | r, | ||
| const df1b2variable & | a, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar in a random effects model |
| a | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |
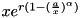
Definition at line 258 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2vector & | r, | ||
| const df1b2variable & | a, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable vector in a random effects model |
| a | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |
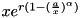
Definition at line 273 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2variable & | r, | ||
| const df1b2vector & | a, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable scalar in a random effects model |
| a | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |
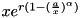
Definition at line 291 of file generalized_Ricker2.cpp.
| df1b2vector generalized_Ricker2 | ( | const dvector & | x, |
| const df1b2vector & | r, | ||
| const df1b2vector & | a, | ||
| const df1b2vector & | alpha | ||
| ) |
generalized Ricker function, second parameerization; random effects vectorized
| x | independent variable; data vector |
| r | ; differentiable vector in a random effects model |
| a | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |
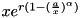
Definition at line 306 of file generalized_Ricker2.cpp.
| dvariable Gompertz | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Gompertz function; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 14 of file Gompertz.cpp.
| dvar_vector Gompertz | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Gompertz function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 30 of file Gompertz.cpp.
| dvar_vector Gompertz | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
Gompertz function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |

Definition at line 46 of file Gompertz.cpp.
| dvar_vector Gompertz | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
Gompertz function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |

Definition at line 63 of file Gompertz.cpp.
| dvar_vector Gompertz | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
Gompertz function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |

Definition at line 79 of file Gompertz.cpp.
| df1b2variable Gompertz | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Gompertz function; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 97 of file Gompertz.cpp.
| df1b2vector Gompertz | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Gompertz function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 111 of file Gompertz.cpp.
| df1b2vector Gompertz | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
Gompertz function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 125 of file Gompertz.cpp.
| df1b2vector Gompertz | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
Gompertz function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 142 of file Gompertz.cpp.
| df1b2vector Gompertz | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
Gompertz function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 156 of file Gompertz.cpp.
| dvariable Hassell | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Hassell function scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
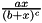
Definition at line 15 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
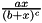
Definition at line 32 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
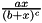
Definition at line 49 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable scalar |
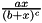
Definition at line 67 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable scalar |
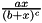
Definition at line 84 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable vector |
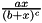
Definition at line 103 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable vector |
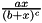
Definition at line 120 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable vector |
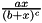
Definition at line 138 of file Hassell.cpp.
| dvar_vector Hassell | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Hassell function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable vector |
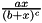
Definition at line 155 of file Hassell.cpp.
| df1b2variable Hassell | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Hassell function random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
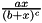
Definition at line 175 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
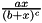
Definition at line 190 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
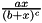
Definition at line 205 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
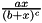
Definition at line 223 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
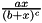
Definition at line 238 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
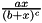
Definition at line 258 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
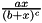
Definition at line 273 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
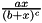
Definition at line 291 of file Hassell.cpp.
| df1b2vector Hassell | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Hassell function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
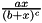
Definition at line 306 of file Hassell.cpp.
| dvariable Hill | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
| dvar_vector Hill | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
| df1b2variable Hill | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
| df1b2vector Hill | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
| dvariable HollingII | ( | const double & | x, |
| const prevariable & | alpha, | ||
| const prevariable & | h | ||
| ) |
HollingII scalar.
| x | independent variable; data scalar |
| alpha | ; differentiable scalar |
| h | ; differentiable scalar |
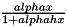
Definition at line 14 of file HollingII.cpp.
| dvar_vector HollingII | ( | const dvector & | x, |
| const prevariable & | alpha, | ||
| const prevariable & | h | ||
| ) |
HollingII vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable scalar |
| h | ; differentiable scalar |
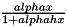
Definition at line 30 of file HollingII.cpp.
| dvar_vector HollingII | ( | const dvector & | x, |
| const dvar_vector & | alpha, | ||
| const prevariable & | h | ||
| ) |
HollingII vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable vector |
| h | ; differentiable scalar |
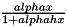
Definition at line 46 of file HollingII.cpp.
| dvar_vector HollingII | ( | const dvector & | x, |
| const prevariable & | alpha, | ||
| const dvar_vector & | h | ||
| ) |
HollingII vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable scalar |
| h | ; differentiable vector |
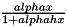
Definition at line 63 of file HollingII.cpp.
| dvar_vector HollingII | ( | const dvector & | x, |
| const dvar_vector & | alpha, | ||
| const dvar_vector & | h | ||
| ) |
HollingII vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable vector |
| h | ; differentiable vector |
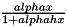
Definition at line 79 of file HollingII.cpp.
| df1b2variable HollingII | ( | const double & | x, |
| const df1b2variable & | alpha, | ||
| const df1b2variable & | h | ||
| ) |
HollingII random effects scalar.
| x | independent variable; data scalar |
| alpha | ; differentiable scalar in a random effects model |
| h | ; differentiable scalar in a random effects model |
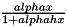
Definition at line 97 of file HollingII.cpp.
| df1b2vector HollingII | ( | const dvector & | x, |
| const df1b2variable & | alpha, | ||
| const df1b2variable & | h | ||
| ) |
HollingII random effects vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable scalar in a random effects model |
| h | ; differentiable scalar in a random effects model |
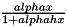
Definition at line 111 of file HollingII.cpp.
| df1b2vector HollingII | ( | const dvector & | x, |
| const df1b2vector & | alpha, | ||
| const df1b2variable & | h | ||
| ) |
HollingII random effects vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable vector in a random effects model |
| h | ; differentiable scalar in a random effects model |
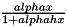
Definition at line 125 of file HollingII.cpp.
| df1b2vector HollingII | ( | const dvector & | x, |
| const df1b2variable & | alpha, | ||
| const df1b2vector & | h | ||
| ) |
HollingII random effects vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable scalar in a random effects model |
| h | ; differentiable vector in a random effects model |
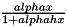
Definition at line 142 of file HollingII.cpp.
| df1b2vector HollingII | ( | const dvector & | x, |
| const df1b2vector & | alpha, | ||
| const df1b2vector & | h | ||
| ) |
HollingII random effects vectorized.
| x | independent variable; data vector |
| alpha | ; differentiable vector in a random effects model |
| h | ; differentiable vector in a random effects model |
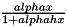
Definition at line 156 of file HollingII.cpp.
| dvariable HollingIII | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Holling Type III function; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 14 of file HollingIII.cpp.
| dvar_vector HollingIII | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Holling Type III function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 30 of file HollingIII.cpp.
| dvar_vector HollingIII | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
Holling Type III function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |

Definition at line 46 of file HollingIII.cpp.
| dvar_vector HollingIII | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
Holling Type III function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |

Definition at line 63 of file HollingIII.cpp.
| dvar_vector HollingIII | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
Holling Type III function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |

Definition at line 79 of file HollingIII.cpp.
| df1b2variable HollingIII | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Holling Type III function; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 97 of file HollingIII.cpp.
| df1b2vector HollingIII | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Holling Type III function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 111 of file HollingIII.cpp.
| df1b2vector HollingIII | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
Holling Type III function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 125 of file HollingIII.cpp.
| df1b2vector HollingIII | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
Holling Type III function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 142 of file HollingIII.cpp.
| df1b2vector HollingIII | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
Holling Type III function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 156 of file HollingIII.cpp.
| dvariable HollingIV | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Holling Type IV function; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
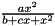
Definition at line 15 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
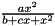
Definition at line 32 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
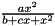
Definition at line 49 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable scalar |
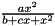
Definition at line 67 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable scalar |
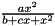
Definition at line 84 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable vector |
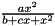
Definition at line 103 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable vector |
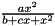
Definition at line 120 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable vector |
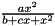
Definition at line 138 of file HollingIV.cpp.
| dvar_vector HollingIV | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Holling Type IV function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable vector |
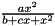
Definition at line 155 of file HollingIV.cpp.
| df1b2variable HollingIV | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Holling Type IV function; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
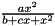
Definition at line 175 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
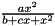
Definition at line 190 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
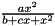
Definition at line 205 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
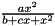
Definition at line 223 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
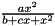
Definition at line 238 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
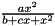
Definition at line 258 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
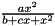
Definition at line 273 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
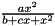
Definition at line 291 of file HollingIV.cpp.
| df1b2vector HollingIV | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Holling Type IV function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
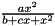
Definition at line 306 of file HollingIV.cpp.
| dvariable logistic | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
logistic function; scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 14 of file ecolib/logistic.cpp.
| dvar_vector logistic | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
logistic function; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 30 of file ecolib/logistic.cpp.
| dvar_vector logistic | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
logistic function; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |

Definition at line 46 of file ecolib/logistic.cpp.
| dvar_vector logistic | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
logistic function; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |

Definition at line 63 of file ecolib/logistic.cpp.
| dvar_vector logistic | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
logistic function; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |

Definition at line 79 of file ecolib/logistic.cpp.
| df1b2variable logistic | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
logistic function; random effects scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 97 of file ecolib/logistic.cpp.
| df1b2vector logistic | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
logistic function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 111 of file ecolib/logistic.cpp.
| df1b2vector logistic | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
logistic function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 125 of file ecolib/logistic.cpp.
| df1b2vector logistic | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
logistic function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 142 of file ecolib/logistic.cpp.
| df1b2vector logistic | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
logistic function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 156 of file ecolib/logistic.cpp.
| dvariable logistic3 | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
logistic function with carrying capacity c; scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | carrying capacity; differentiable scalar |

Definition at line 15 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | carrying capacity; differentiable scalar |

Definition at line 32 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | carrying capacity; differentiable scalar |

Definition at line 49 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | carrying capacity; differentiable scalar |

Definition at line 67 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | carrying capacity; differentiable scalar |

Definition at line 84 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | carrying capacity; differentiable vector |

Definition at line 103 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | carrying capacity; differentiable vector |

Definition at line 120 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | carrying capacity; differentiable vector |

Definition at line 138 of file logistic3.cpp.
| dvar_vector logistic3 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
logistic function with carrying capacity c; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | carrying capacity; differentiable vector |

Definition at line 155 of file logistic3.cpp.
| df1b2variable logistic3 | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
logistic function with carrying capacity c; random effects scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | carrying capacity; differentiable scalar in a random effects model |

Definition at line 175 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | carrying capacity; differentiable scalar in a random effects model |

Definition at line 190 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | carrying capacity; differentiable scalar in a random effects model |

Definition at line 205 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | carrying capacity; differentiable scalar in a random effects model |

Definition at line 223 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | carrying capacity; differentiable scalar in a random effects model |

Definition at line 238 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | carrying capacity; differentiable vector in a random effects model |

Definition at line 258 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | carrying capacity; differentiable vector in a random effects model |

Definition at line 273 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | carrying capacity; differentiable vector in a random effects model |

Definition at line 291 of file logistic3.cpp.
| df1b2vector logistic3 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
logistic function with carrying capacity c; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | carrying capacity; differentiable vector in a random effects model |

Definition at line 306 of file logistic3.cpp.
| dvariable logisticK | ( | const double & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; scalar
| t | independent variable; data scalar |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | initial population size at t=0; differentiable scalar |
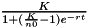
Definition at line 15 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | initial population size at t=0; differentiable scalar |
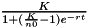
Definition at line 32 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable scalar |
| n0 | initial population size at t=0; differentiable scalar |
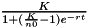
Definition at line 49 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const dvar_vector & | r, | ||
| const prevariable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable vector |
| n0 | initial population size at t=0; differentiable scalar |
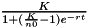
Definition at line 67 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const dvar_vector & | r, | ||
| const prevariable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable vector |
| n0 | initial population size at t=0; differentiable scalar |
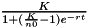
Definition at line 84 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const dvar_vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | initial population size at t=0; differentiable vector |
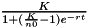
Definition at line 103 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const prevariable & | r, | ||
| const dvar_vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable scalar |
| n0 | initial population size at t=0; differentiable vector |
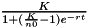
Definition at line 120 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const dvar_vector & | r, | ||
| const dvar_vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable vector |
| n0 | initial population size at t=0; differentiable vector |
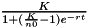
Definition at line 138 of file logisticK.cpp.
| dvar_vector logisticK | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const dvar_vector & | r, | ||
| const dvar_vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable vector |
| n0 | initial population size at t=0; differentiable vector |
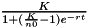
Definition at line 155 of file logisticK.cpp.
| df1b2variable logisticK | ( | const double & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects scalar
| t | independent variable; data scalar |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | initial population size at t=0; differentiable scalar in a random effects model |
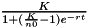
Definition at line 175 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | initial population size at t=0; differentiable scalar in a random effects model |
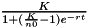
Definition at line 190 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | initial population size at t=0; differentiable scalar in a random effects model |
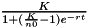
Definition at line 205 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2variable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | initial population size at t=0; differentiable scalar in a random effects model |
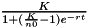
Definition at line 223 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2variable & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | initial population size at t=0; differentiable scalar in a random effects model |
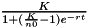
Definition at line 238 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | initial population size at t=0; differentiable vector in a random effects model |
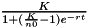
Definition at line 258 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | initial population size at t=0; differentiable vector in a random effects model |
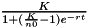
Definition at line 273 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | initial population size at t=0; differentiable vector in a random effects model |
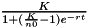
Definition at line 291 of file logisticK.cpp.
| df1b2vector logisticK | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2vector & | n0 | ||
| ) |
ecologically parameterized logistic function with carrying capacity K; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | initial population size at t=0; differentiable vector in a random effects model |
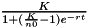
Definition at line 306 of file logisticK.cpp.
| dvariable Michaelis_Menten1 | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
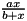
Definition at line 14 of file Michaelis_Menten1.cpp.
| dvar_vector Michaelis_Menten1 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
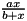
Definition at line 30 of file Michaelis_Menten1.cpp.
| dvar_vector Michaelis_Menten1 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
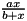
Definition at line 46 of file Michaelis_Menten1.cpp.
| dvar_vector Michaelis_Menten1 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
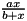
Definition at line 63 of file Michaelis_Menten1.cpp.
| dvar_vector Michaelis_Menten1 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
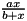
Definition at line 79 of file Michaelis_Menten1.cpp.
| df1b2variable Michaelis_Menten1 | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
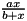
Definition at line 97 of file Michaelis_Menten1.cpp.
| df1b2vector Michaelis_Menten1 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
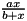
Definition at line 111 of file Michaelis_Menten1.cpp.
| df1b2vector Michaelis_Menten1 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
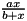
Definition at line 125 of file Michaelis_Menten1.cpp.
| df1b2vector Michaelis_Menten1 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
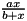
Definition at line 142 of file Michaelis_Menten1.cpp.
| df1b2vector Michaelis_Menten1 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
Michaelis Menten function, 1st parametarization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
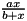
Definition at line 156 of file Michaelis_Menten1.cpp.
| dvariable Michaelis_Menten2 | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 14 of file Michaelis_Menten2.cpp.
| dvar_vector Michaelis_Menten2 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |

Definition at line 30 of file Michaelis_Menten2.cpp.
| dvar_vector Michaelis_Menten2 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |

Definition at line 46 of file Michaelis_Menten2.cpp.
| dvar_vector Michaelis_Menten2 | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |

Definition at line 63 of file Michaelis_Menten2.cpp.
| dvar_vector Michaelis_Menten2 | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |

Definition at line 79 of file Michaelis_Menten2.cpp.
| df1b2variable Michaelis_Menten2 | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 97 of file Michaelis_Menten2.cpp.
| df1b2vector Michaelis_Menten2 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 111 of file Michaelis_Menten2.cpp.
| df1b2vector Michaelis_Menten2 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |

Definition at line 125 of file Michaelis_Menten2.cpp.
| df1b2vector Michaelis_Menten2 | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 142 of file Michaelis_Menten2.cpp.
| df1b2vector Michaelis_Menten2 | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
Michaelis Menten function, 2nd parameterization; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |

Definition at line 156 of file Michaelis_Menten2.cpp.
| dvariable monomolecular | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
monomoleular function; scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
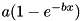
Definition at line 14 of file monomolecular.cpp.
| dvar_vector monomolecular | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
monomoleular function; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
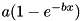
Definition at line 30 of file monomolecular.cpp.
| dvar_vector monomolecular | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
monomoleular function; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
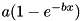
Definition at line 46 of file monomolecular.cpp.
| dvar_vector monomolecular | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
monomoleular function; vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
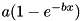
Definition at line 63 of file monomolecular.cpp.
| dvar_vector monomolecular | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
monomoleular function; vectorized
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
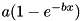
Definition at line 79 of file monomolecular.cpp.
| df1b2variable monomolecular | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
monomoleular function; random effects scalar
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
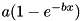
Definition at line 97 of file monomolecular.cpp.
| df1b2vector monomolecular | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
monomoleular function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
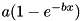
Definition at line 111 of file monomolecular.cpp.
| df1b2vector monomolecular | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
monomoleular function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
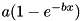
Definition at line 125 of file monomolecular.cpp.
| df1b2vector monomolecular | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
monomoleular function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
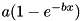
Definition at line 142 of file monomolecular.cpp.
| df1b2vector monomolecular | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
monomoleular function; random effects vectorized
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
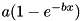
Definition at line 156 of file monomolecular.cpp.
| dvariable nonrectangular_hyperbola | ( | const double & | x, |
| const prevariable & | theta, | ||
| const prevariable & | alpha, | ||
| const prevariable & | pmax | ||
| ) |
nonrectangular hyperbolic function; scalar
| x | independent variable; data scalar |
| theta | ; differentiable scalar |
| alpha | ; differentiable scalar |
| pmax | ; differentiable scalar |

Definition at line 15 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const prevariable & | theta, | ||
| const prevariable & | alpha, | ||
| const prevariable & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar |
| alpha | ; differentiable scalar |
| pmax | ; differentiable scalar |

Definition at line 32 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const dvar_vector & | theta, | ||
| const prevariable & | alpha, | ||
| const prevariable & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector |
| alpha | ; differentiable scalar |
| pmax | ; differentiable scalar |

Definition at line 49 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const prevariable & | theta, | ||
| const dvar_vector & | alpha, | ||
| const prevariable & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar |
| alpha | ; differentiable vector |
| pmax | ; differentiable scalar |

Definition at line 67 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const dvar_vector & | theta, | ||
| const dvar_vector & | alpha, | ||
| const prevariable & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector |
| alpha | ; differentiable vector |
| pmax | ; differentiable scalar |

Definition at line 84 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const prevariable & | theta, | ||
| const prevariable & | alpha, | ||
| const dvar_vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar |
| alpha | ; differentiable scalar |
| pmax | ; differentiable vector |

Definition at line 103 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const dvar_vector & | theta, | ||
| const prevariable & | alpha, | ||
| const dvar_vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector |
| alpha | ; differentiable scalar |
| pmax | ; differentiable vector |

Definition at line 120 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const prevariable & | theta, | ||
| const dvar_vector & | alpha, | ||
| const dvar_vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar |
| alpha | ; differentiable vector |
| pmax | ; differentiable vector |

Definition at line 138 of file nonrectangular_hyperbola.cpp.
| dvar_vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const dvar_vector & | theta, | ||
| const dvar_vector & | alpha, | ||
| const dvar_vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector |
| alpha | ; differentiable vector |
| pmax | ; differentiable vector |

Definition at line 155 of file nonrectangular_hyperbola.cpp.
| df1b2variable nonrectangular_hyperbola | ( | const double & | x, |
| const df1b2variable & | theta, | ||
| const df1b2variable & | alpha, | ||
| const df1b2variable & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects scalar
| x | independent variable; data scalar |
| theta | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
| pmax | ; differentiable scalar in a random effects model |

Definition at line 175 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2variable & | theta, | ||
| const df1b2variable & | alpha, | ||
| const df1b2variable & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
| pmax | ; differentiable scalar in a random effects model |

Definition at line 190 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2vector & | theta, | ||
| const df1b2variable & | alpha, | ||
| const df1b2variable & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
| pmax | ; differentiable scalar in a random effects model |

Definition at line 205 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2variable & | theta, | ||
| const df1b2vector & | alpha, | ||
| const df1b2variable & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |
| pmax | ; differentiable scalar in a random effects model |

Definition at line 223 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2vector & | theta, | ||
| const df1b2vector & | alpha, | ||
| const df1b2variable & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |
| pmax | ; differentiable scalar in a random effects model |

Definition at line 238 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2variable & | theta, | ||
| const df1b2variable & | alpha, | ||
| const df1b2vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
| pmax | ; differentiable vector in a random effects model |

Definition at line 258 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2vector & | theta, | ||
| const df1b2variable & | alpha, | ||
| const df1b2vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector in a random effects model |
| alpha | ; differentiable scalar in a random effects model |
| pmax | ; differentiable vector in a random effects model |

Definition at line 273 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2variable & | theta, | ||
| const df1b2vector & | alpha, | ||
| const df1b2vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable scalar in a random effects model |
| alpha | ; differentiable vector in a random effects model |
| pmax | ; differentiable vector in a random effects model |

Definition at line 291 of file nonrectangular_hyperbola.cpp.
| df1b2vector nonrectangular_hyperbola | ( | const dvector & | x, |
| const df1b2vector & | theta, | ||
| const df1b2vector & | alpha, | ||
| const df1b2vector & | pmax | ||
| ) |
nonrectangular hyperbolic function; random effects vectorized
| x | independent variable; data vector |
| theta | ; differentiable vector in a random effects model |
| alpha | ; differentiable vector in a random effects model |
| pmax | ; differentiable vector in a random effects model |

Definition at line 306 of file nonrectangular_hyperbola.cpp.
| dvariable Ricker | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Ricker function; scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
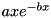
Definition at line 14 of file Ricker.cpp.
| dvar_vector Ricker | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b | ||
| ) |
Ricker function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
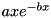
Definition at line 30 of file Ricker.cpp.
| dvar_vector Ricker | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b | ||
| ) |
Ricker function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
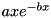
Definition at line 46 of file Ricker.cpp.
| dvar_vector Ricker | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b | ||
| ) |
Ricker function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
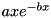
Definition at line 63 of file Ricker.cpp.
| dvar_vector Ricker | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b | ||
| ) |
Ricker function; vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
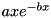
Definition at line 79 of file Ricker.cpp.
| df1b2variable Ricker | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Ricker function; random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
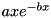
Definition at line 97 of file Ricker.cpp.
| df1b2vector Ricker | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b | ||
| ) |
Ricker function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
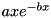
Definition at line 111 of file Ricker.cpp.
| df1b2vector Ricker | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b | ||
| ) |
Ricker function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
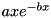
Definition at line 125 of file Ricker.cpp.
| df1b2vector Ricker | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b | ||
| ) |
Ricker function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
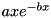
Definition at line 142 of file Ricker.cpp.
| df1b2vector Ricker | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b | ||
| ) |
Ricker function; random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
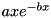
Definition at line 156 of file Ricker.cpp.
| dvariable Shepherd | ( | const double & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Shepherd function scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
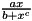
Definition at line 15 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
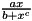
Definition at line 32 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const prevariable & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable scalar |
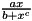
Definition at line 49 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable scalar |
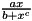
Definition at line 67 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const prevariable & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable scalar |
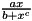
Definition at line 84 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable scalar |
| c | ; differentiable vector |
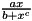
Definition at line 103 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const prevariable & | b, | ||
| const dvar_vector & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable scalar |
| c | ; differentiable vector |
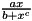
Definition at line 120 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const prevariable & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar |
| b | ; differentiable vector |
| c | ; differentiable vector |
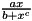
Definition at line 138 of file Shepherd.cpp.
| dvar_vector Shepherd | ( | const dvector & | x, |
| const dvar_vector & | a, | ||
| const dvar_vector & | b, | ||
| const dvar_vector & | c | ||
| ) |
Shepherd function vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector |
| b | ; differentiable vector |
| c | ; differentiable vector |
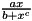
Definition at line 155 of file Shepherd.cpp.
| df1b2variable Shepherd | ( | const double & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Shepherd function random effects scalar.
| x | independent variable; data scalar |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
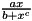
Definition at line 175 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
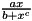
Definition at line 190 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2variable & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable scalar in a random effects model |
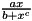
Definition at line 205 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
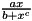
Definition at line 223 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2variable & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable scalar in a random effects model |
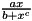
Definition at line 238 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
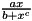
Definition at line 258 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2variable & | b, | ||
| const df1b2vector & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable scalar in a random effects model |
| c | ; differentiable vector in a random effects model |
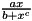
Definition at line 273 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2variable & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable scalar in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
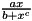
Definition at line 291 of file Shepherd.cpp.
| df1b2vector Shepherd | ( | const dvector & | x, |
| const df1b2vector & | a, | ||
| const df1b2vector & | b, | ||
| const df1b2vector & | c | ||
| ) |
Shepherd function random effects vectorized.
| x | independent variable; data vector |
| a | ; differentiable vector in a random effects model |
| b | ; differentiable vector in a random effects model |
| c | ; differentiable vector in a random effects model |
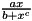
Definition at line 306 of file Shepherd.cpp.
| dvariable theta_logistic | ( | const double & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; scalar
| t | independent variable; data scalar |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | population size at t=0; differentiable scalar |

Definition at line 15 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | population size at t=0; differentiable scalar |

Definition at line 32 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const prevariable & | r, | ||
| const prevariable & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable scalar |
| n0 | population size at t=0; differentiable scalar |

Definition at line 49 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const dvar_vector & | r, | ||
| const prevariable & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable vector |
| n0 | population size at t=0; differentiable scalar |

Definition at line 67 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const dvar_vector & | r, | ||
| const prevariable & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable vector |
| n0 | population size at t=0; differentiable scalar |

Definition at line 84 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const prevariable & | r, | ||
| const dvar_vector & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable scalar |
| n0 | population size at t=0; differentiable vector |

Definition at line 103 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const prevariable & | r, | ||
| const dvar_vector & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable scalar |
| n0 | population size at t=0; differentiable vector |

Definition at line 120 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const prevariable & | K, | ||
| const dvar_vector & | r, | ||
| const dvar_vector & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar |
| r | growth rate; differentiable vector |
| n0 | population size at t=0; differentiable vector |

Definition at line 138 of file theta_logistic.cpp.
| dvar_vector theta_logistic | ( | const dvector & | t, |
| const dvar_vector & | K, | ||
| const dvar_vector & | r, | ||
| const dvar_vector & | n0, | ||
| const prevariable & | theta | ||
| ) |
theta logistic function; vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector |
| r | growth rate; differentiable vector |
| n0 | population size at t=0; differentiable vector |

Definition at line 155 of file theta_logistic.cpp.
| df1b2variable theta_logistic | ( | const double & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects scalar
| t | independent variable; data scalar |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | population size at t=0; differentiable scalar in a random effects model |

Definition at line 175 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | population size at t=0; differentiable scalar in a random effects model |

Definition at line 190 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2variable & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | population size at t=0; differentiable scalar in a random effects model |

Definition at line 205 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2variable & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | population size at t=0; differentiable scalar in a random effects model |

Definition at line 223 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2variable & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | population size at t=0; differentiable scalar in a random effects model |

Definition at line 238 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2vector & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | population size at t=0; differentiable vector in a random effects model |

Definition at line 258 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2variable & | r, | ||
| const df1b2vector & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable scalar in a random effects model |
| n0 | population size at t=0; differentiable vector in a random effects model |

Definition at line 273 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2variable & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2vector & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable scalar in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | population size at t=0; differentiable vector in a random effects model |

Definition at line 291 of file theta_logistic.cpp.
| df1b2vector theta_logistic | ( | const dvector & | t, |
| const df1b2vector & | K, | ||
| const df1b2vector & | r, | ||
| const df1b2vector & | n0, | ||
| const df1b2variable & | theta | ||
| ) |
theta logistic function; random effects vectorized
| t | independent variable; data vector |
| K | carrying capacity; differentiable vector in a random effects model |
| r | growth rate; differentiable vector in a random effects model |
| n0 | population size at t=0; differentiable vector in a random effects model |

Definition at line 306 of file theta_logistic.cpp.
|
|
Generated on Tue Mar 8 2016 19:51:38 for ADMB Documentation by  1.8.0 1.8.0
|